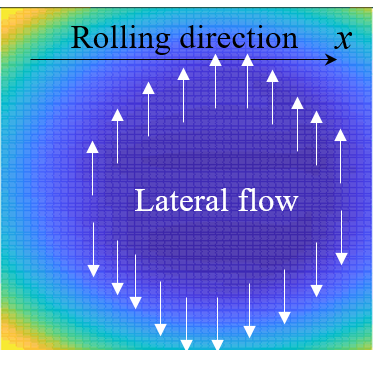
假设
相比于NS方程,Reynolds方程作出了如下基本假设[1]:
- 忽略体积力(如重力、磁力等)的作用
- 流体在界面上无滑动,即贴于表面的流体速度与表面速度相同
- 在沿润滑膜厚度方向不计压力的变化。由于膜厚仅几十微米或更小,压力不会发生明显的变化。
- 与油膜厚度相比较,轴承表面的曲率半径很大,因而忽略油膜曲率的影响,并用平移速度代替转动速度。
- 润滑剂是牛顿流体,对于一般工况条件下使用的矿物油而言是合理的。
- 流动为层流,油膜中不存在涡流和湍流。对于高速大型轴承,可能处于湍流润滑。
- 与粘性力比较,可忽略惯性力的影响。
Reynolds方程
根据上述假设,得出两种Reynolds方程形式:
- 温诗铸等[1]
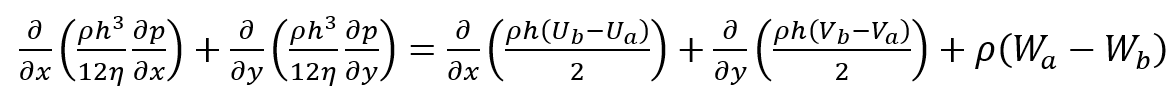
- Bhushan等[2]
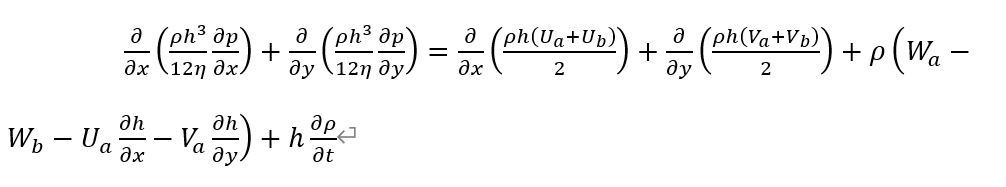
两个式子相同符号的物理含义一致,其中x、y代表参考系的x、y方向,ρ代表油膜密度,η为润滑油粘度,h为油膜厚度,p为油膜压强,U、V、W分别代表润滑油上下表面沿x、y、z方向的运动速度,下标a和b分别代表上下表面。
当以下等式成立时:

以上两个Reynolds方程:温诗铸等[1]=Bhushan等[2]
简单(稳态)工况
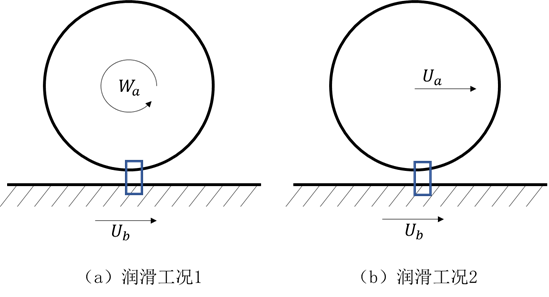
与油膜厚度相比较,轴承表面的曲率半径很大,因而忽略油膜曲率的影响,并用平移速度代替转动速度
方程书写
润滑工况:

方程推导
因为方程的不一致容易给研究学者带来困惑,因此本文对Reynolds进行了推导,分析当前工程问题所用到的Reynolds方程形式,并对不同形式的Reynolds进行比较。
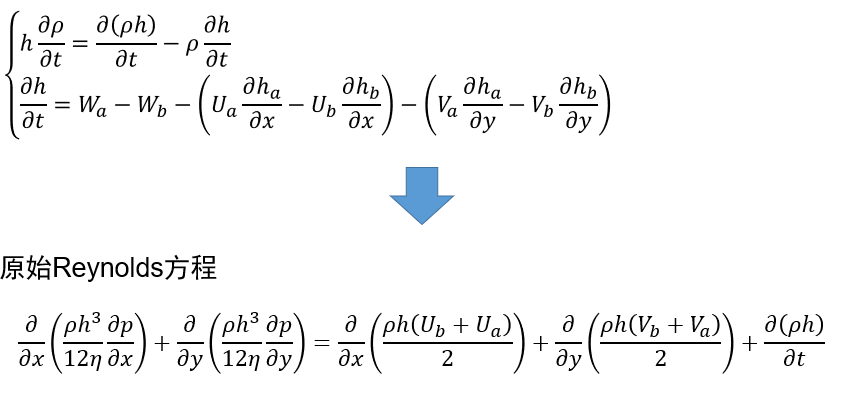
取空间一控制体,润滑油流入流出控制体满足连续性方程,且对每一个控制体在油膜厚度上积分,可得如下两个式子:

上式中油膜厚度,、分别代表油膜上下表面在坐标系中的高度。
需要注意的是式中的Wa、Wb,即润滑油上下表面在z方向的运动速度,根据假设b得知该速度就是上下表面物体的运动速度,对于动压润滑状态该速度可直接由物体的质心速度和旋转速度求解得到,而对于弹流动压润滑计算,这两个速度(Wh、Wo)应包括材料弹性形变产生的速度,在工程上难于直接计算。应用如下变换可以得到Reynolds方程:
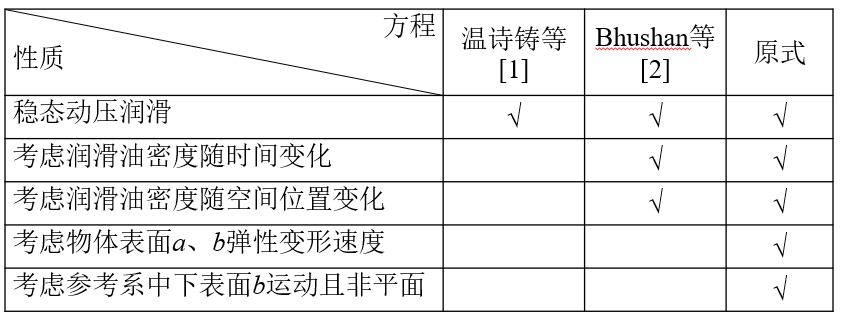
方程比较
[1]. 温诗铸, 黄平, 田煜等. 摩擦学原理(第5版)[M/OL]. 温诗铸, 黄平, 田煜等, 编//清华大学出版社. 第五版 版. 北京: 清华大学出版社, 2019[2020–12–22]. http://spu.dangdang.com/1228019185.html.
[2]. BHUSHAN B. Principles and applications of tribology[M/OL]. second edi 版. New York: Wiley, 2013[2020–12–22]. https://cds.cern.ch/record/1616999.